滑車は、中央に1つの軸を持つ円盤で構成されたもので、シーブ又はプーリーと呼ばれています。滑車には溝が設けられ、そこにロープ等を掛けて使用しています。
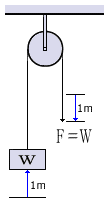
クレーンのトロリ、移動式クレーンのジブ等に使用されている滑車を「定滑車」 という。定滑車は、滑車が定位置に固定されているためロープを引っ張っても滑車の位置は変わらない。ロープの一端に荷を結び、もう一方のロープを引っ張って荷を1mつり上げるためには、ロープを1m引っ張る必要がある。定滑車は、ロープを引っ張る力の方向を変えることはできるが、力の大きさ(F)を変えることはできない。

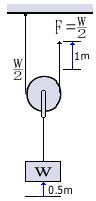
クレーンや移動式クレーン等のフックブロックに使用されている滑車装置を「動滑車」という。動滑車の軸は固定されていないため、ロープを引っ張ると滑車装置も上下する。動滑車のロープを引っ張る方向は、つり荷が動く方向と同じであるため、ロープを引っ張る方向は変わらない。滑車やロープの重さを考えなければ動滑車1個で荷をつり上げるために必要な力(F)は、つり荷の質量の2分の1になる。ただし、動滑車で荷を1mつり上げるためには、ロープを2m引っ張る必要がある。

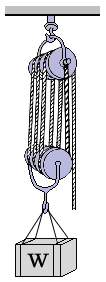
幾つかの動滑車と定滑車を組み合せたものを「組み合せ滑車(滑車装置)」という。組み合せ滑車は、小さな力で質量のある荷をつり上げることができる。たとえば、定滑車3個と動滑車3個を組み合せた滑車装置の場合、滑車の質量や摩擦を考えなければ、荷の質量の1/6の力で荷をつり上げることができる。ただし、ロープを1m 引っ張っても、引っ張った長さの1/6 しか荷は上がらない。
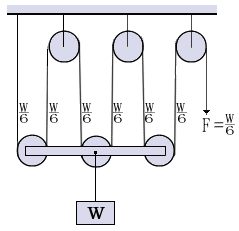
滑車装置を用いて荷をつり上げる時に必要な最小の力(F)は、次の式で求めることができる。なお、つり荷の質量に動滑車の質量の質量を加える必要がある場合は、式の中の(つり荷の質量)を(つり荷の質量+動滑車の質量)とする。また、動滑車に働く荷重を支えるロープ数とは、図の動滑車の①や②等のロープの本数をいうものである。

定滑車は、力の大きさに影響を与えない。したがって、滑車装置を用いて荷をつり上げる時に必要な最小の力を求める時は、定滑車は無視して構わない。 クレーン等の参考書には、「動滑車に働く荷重を支えるロープ数」ではなく、「動滑車×2」 としているものがある。一見、正しいように思えるが、次のような滑車装置には当てはまらない。図の滑車装置に動滑車×2 の式を当てはめると、誤った答えになる。
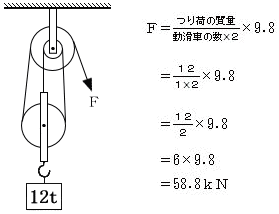
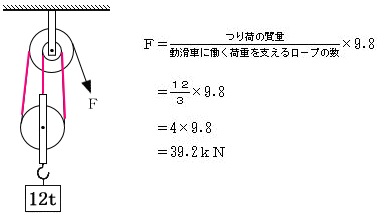
このような滑車装置は、動滑車に働く荷重を支えるロープ数によって、荷をつり上げる時に必要な最小の力を求めなくてはならない。正しくは、次の式になる。最悪ともいえる参考書の場合、つり荷の質量を定滑車と動滑車の数で除して求めるとしているものもある。まぐれで正解になることもあり得るが、唖然とする解説である。おそらく、手当たり次第に様々な分野の本の中身を抜き出して出版している業者が書いたものと思われる。クレーン等の書籍を購入される際は、このような所をチェックするのが賢明である。
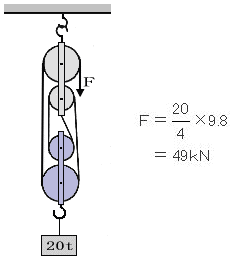
<例題>
次の図のような組み合せ滑車を用いて質量20tの荷をつり上げる時に必要な最小の力F(KN)の求め方。ただし、滑車の質量と摩擦は考えないものとする。動滑車に働く荷重を支えるロープ数は、4本。したがって、Fの値は
図Aのようにロープの端が次々と別の動滑車につられている場合は、「滑車装置1」で説明した式を用いることはできない。図Bの滑車装置に「滑車装置1」の式を当てはめると、荷をつるために必要な最小の力Fは、W/6になる。しかし、この図で分かる通り、ロープの端が次々と別の動滑車につられている場合は、W/8になる。したがって、このような滑車装置の場合は、各ロープに働く荷重を順に追って求める、あるいは次の式によって求めなくてはならない。
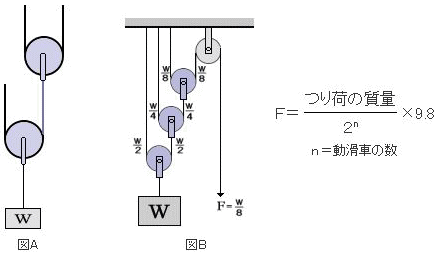
<例題>
図のような組み合せ滑車を用いて質量18tの荷をつり上げる時に必要な最小の力Fの求め方。ただし、滑車の質量及び摩擦は考えないものとする。動滑車に働く荷重を支えるロープに掛かる荷重を順に追って求めると、上記の図Bのように荷をつるために必要な最小の力はW/8になる。式を用いる場合は、次のように解ことができる。このような滑車装置に「滑車装置1」の式を用いた場合は、F=18/6×9.8=29.4kNとなるため、注意しなければならない。