


外力、内力、モーメント等は、変形する物体を取扱う材料力学に使用されています。クレーン等は、どのような設計なら壊れないのか、どのような扱いをすると変形するのかを考えなければなりません。これらの問いに答えるものが材料力学です。材料力学という用語は、材料と力学の合成語で、材料と力学の2つの分野の知識で成り立っています。
物体に作用する外部からの力を「荷重」という。その荷重には、引張荷重や圧縮荷重等がある。力学において物体に作用する力を考える場合、外力と内力を区別する必要がある。荷重(外力)は、力の掛かり方よって分類することができる。力の作用を分布状態によって分類する場合、狭い範囲に集中して作用する「集中荷重」と、広い範囲に広がって作用する「分布荷重」に分けることができる。
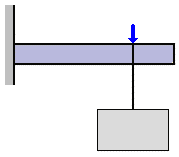
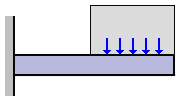
荷重を力の向きによって分けると、次のように分類することができる。
物体を引き伸ばすように働く荷重
1. クレーン等の巻上用ワイヤロープの直線部分に掛かる荷重
2. 玉掛用ワイヤロープの直線部分に掛かる荷重
3. ガイデリックのブームの反対側のガイロープに掛かる荷重
4. ジンポールデリックのガイロープに掛かる荷重
物体を押し縮めるように働く荷重
1. 横行レール、走行レール等が車輪によって受ける荷重
2. 橋形クレーンの振脚に掛かる荷重
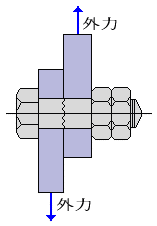
物体を横からハサミで切るように働く荷重
1. 2枚の鋼板を締め付けているボルト、リベット、キー等を荷重方向に切断しようとする荷重
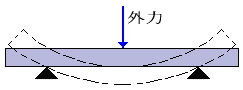
物体を曲げるように働く荷重
1. ジブを曲げようとする荷重
物体をねじるように働く荷重
1. 動力を伝えるウインチの回転軸に働く荷重
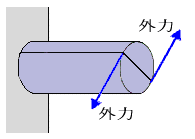
クレーン等の機械部分の多くは、引張荷重、圧縮荷重、曲げ荷重、ねじり荷重が複合的に組み合されている。
1. 動力軸(曲げ荷重とねじり荷重)
2. クレーンガーダ(曲げ荷重とねじり荷重)
3. ジブ(圧縮荷重と曲げ荷重)
4. ドラム(圧縮荷重と曲げ荷重)
5. フック(引張荷重と曲げ荷重)
6. ドラム部分のワイヤロープ(引張荷重と曲げ荷重)
7. シーブ部分のワイヤロープ(引張荷重と曲げ荷重)
8. スチフレッグデリックのステー(引張荷重と圧縮荷重)
荷重を力の掛かる速度によって分けると、次のように分類することができる。
静荷重は、力の大きさと向きが変わらない荷重で、死荷重とも呼ばれる。力学において自重(クレーンや材料そのもの自体の重さ)を考える場合、重力は物体に働く外力として作用している。
1. クレーン本体の自重
2. 荷をつり上げて静止している状態の荷重
動荷重は、力の大きさと方向が変化する荷重で、活荷重とも呼ばれる。また、動荷重は、衝撃荷重と繰返し荷重に分けることができる。
○ 衝撃荷重
つり荷を巻下げている時に急制動した場合、または玉掛用ワイヤロープが緩んでいる状態から全速で巻上げた場合は、つり荷よりも大きな荷重がワイヤロープに作用して切断することがある。このような場合に発生する荷重を「衝撃荷重」という。衝撃荷重は、ハンマーで物を叩くように急激な力が極めて短時間に加わる荷重で、本来の荷重よりも大きな力が作用する。
1. つり荷の巻上げや巻下げを急激に行った時に作用する荷重
2. クレーンの運動を急激に停止する時に作用する荷重
○ 繰返し荷重
繰返し荷重には、荷重の向きは同じで荷重の大きさが時間と共に変化する「片振り荷重」と、荷重の向きと大きさが時間と共に変化する「両振り荷重(交番荷重)」がある。繰返し荷重は、静荷重よりも小さな力でクレーンの構造部分を疲労させて破壊させることがある。このような破壊現象を「疲労破壊」という。
1. 片振り荷重(クレーンのワイヤロープやウインチの軸受等に作用する荷重)
2. 両振り荷重(歯車軸に作用する荷重)
物体に荷重が作用する時、物体内部にその荷重に抵抗してつり合いを保とうとする力が生じる。この内力を「応力」という 。応力は荷重に等しく、向きは反対になる。応力について考える場合は、図のように物体を仮想的に切断して2つの面を作り、内力の方向と作用している面の両方について考える必要がある。

応力には、引張応力、圧縮応力、せん断応力等がある。応力は、部材に作用する荷重を部材の断面積で除した単位面積当たりの力の大きさで求めることができ、単位にはn/mm2が用いられている。なお、曲げ応力やねじり応力の場合は、部材に荷重が均等に作用しないため、これらの応力は簡単に求めることができない。
<例題>
7cm×10cmの長方形断面の鋼材に14kNの圧縮荷重が作用する時の圧縮応力の求め方。
応力の単位は、n/mm2。したがって、長方形の断面積をmm2の単位に、圧縮荷重をNの単位にして圧縮応力を求める。
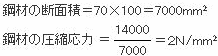
物体に引張荷重や圧縮荷重等の外力が加わると、物体に変形が生じる。引張荷重は、ゴムを伸ばしたような変形を生じさせる。圧縮荷重は、堅いボールを圧縮させたような変形を生じさせる。物体の原型に対する変形の割合を「ひずみ」といい、引張荷重による「引張ひずみ」や圧縮荷重による「圧縮ひずみ」等がある。材料の軸方向に荷重が加わって生じる変形量と元の長さの比を「縦ひずみ」といい、イプシロン(ε)で表す。物体の元の長さをL1、変形量をL2とすると、ひずみは次の式で求めることができる。
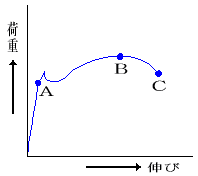
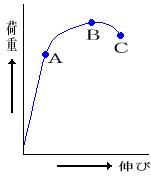
ひずみは、材料の断片である試験片を材料試験機に掛け、徐々に荷重を加えて調べる。下の図は、応力とひずみをグラフで表したもので、「応力―ひずみ曲線」と呼ばれている。この図において、材料の試験片を静かにA点まで荷重を掛けて引っ張ると試験片は変形して伸びるが荷重を加えるのを止めると元の長さに戻る。このように変形した材料が元に戻る性質を「弾性」という。変形量の小さい弾性領域内においての応力とひずみは比例し、荷重を取り除くとひずみは消失する。しかし、それ以上の荷重を加えてA点の弾性限度を超えた場合は試験片は元に戻らず、変形が更に大きくなって荷重が最大のB点に達する。B点の荷重は、この材料に掛けることができる最大の荷重で、この値を試験片の断面積で除した応力を「引張強さ」 という。また、元に戻らなくなったひずみは「永久ひずみ」という。B点以降は、荷重を増加しなくても試験片の伸びが更に増大し、C点に達して切断する。このB点の試験片が切断するまでに掛けられる最大の荷重を「切断荷重(JISでは破断荷重という。)」といい、材料によって決まった値を有している。

クレーン等に実際に生じる応力を「使用応力」 といい、部材の変形や破壊に至らない安全と考えられる応力の最大値を「許容応力」という。この許容応力は、一般に次の式によって求めることができる。クレーン等の構造部分の部材は、変形や破壊が生じない範囲で使用しなければならない。各部材に生じる応力は、荷重の大きさや作業状態によって変化する。また、衝撃荷重が作用することもあるため、応力を正確に把握することは極めて困難である。このため、クレーン等構造規格において使用条件、部材の性質、荷重の種類による許容応力の値を算出する計算式を定め、これをクレーン、デリック、移動式クレーンの設計の基としている。