重心とは、質量が分布する空間において、その質量に対して他の物体から働く万有引力の合力の作用点です。したがって、重心は質量中心であるともいえます。
物体は小さな分子で構成され、それぞれの分子には重力が作用している。これらの重力が1点に集中して働く作用点を「重心」という。物体の重心は常に一定の点で、物体の位置や置き方を変えても物体の重心の位置は変わらない。また、物体の材料が異なっていても、形状が同じで材質が均一であれば、重心は同じ位置にある。ただし、重心が必ずしも物体内部にあるとは限らない。
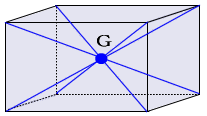
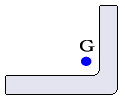
簡単な形状の物体や、その組み合せである物体は、分割してそれぞれの重心を求め、その合力によって物体全体の重心を求めることができる。図のような形状の物体は、AとBの2つに分け、それぞれの対角線の交点によって重心G1、G2を求める。次にAの重心G1から任意の直線G1、Dを引き、更にG1、D上で質量比を逆にした点Cを求める。続いて点cからD、G2 に平行な直線C、Gを引き、G1、G2と交わる交点を求める。これにより、形状の異なる物体の重心Gを求めることができる。
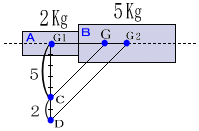
図式によって重心を求めることができる物体は、数式でも重心を求めることができる。図のような物体は、AとBに分け、それぞれの対角線の交点によって重心G1とG2を求める。Aの質量をW1、Bの質量をW2とすると、Aの重心G1から物体の重心Gまでのaの長さ及びBの重心G2から物体の重心Gまでのbの長さは、平行力のつり合いにより、次の式で求めることができる。
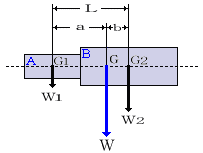
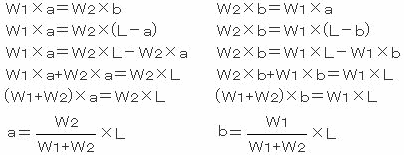
<例題>
図のような物体Aの質量が20kg、物体Bの質量が70kg、AとBの重心間の長さが90cm場合の重心GからG2までの長さ(X)の求め方。
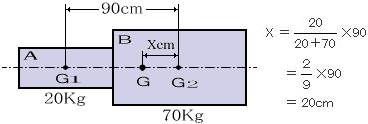
物体を1点でつった時、その鉛直線は必ず物体の重心を通る。互いに物体の異なる任意の箇所をつり、その作用線の交点を求めると、物体の重心を求めることができる。
クレーン等の作業では、重心位置が図Aのように偏っている状態で荷をつると、つり荷は図Bのように傾く。これは、F1とF2がつり合おうとしてズレを修正するために起きるもので、この傾いた状態でF1とF2はつり合っている。
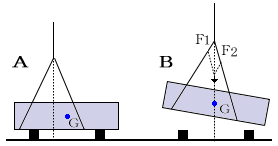
傾いた状態で荷をつった場合、左右のワイヤロープに作用する張力が異なるため、一方の玉掛用ワイヤロープに大きな負荷が掛かる。荷の傾きは、ワイヤロープの滑りや荷の落下の原因になるため、クレーン等を用いて荷をつり上げる時は、荷の重心の真上にフックを移動させ、つり荷を水平につらなければならない。玉掛作業においては、次の手順に従って玉掛けを行うことが大切である。
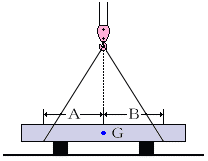
1. 目安により荷の重心位置を定め、玉掛けを行う。その際、同じ長さのワイヤロープを使用
し、AとBの間隔も同じ長さにする。
2. 荷を少しつり上げ、荷の状態を確認する。
3. つり荷が傾く場合は、一旦、荷を下ろし、荷が下がっている方向にフック及び玉掛用ワイヤ
ロープをずらす。
4. 再度、荷をつり上げて確認する。
5. つり荷が安定しない場合は、水平になるまでこの手順を繰り返す。
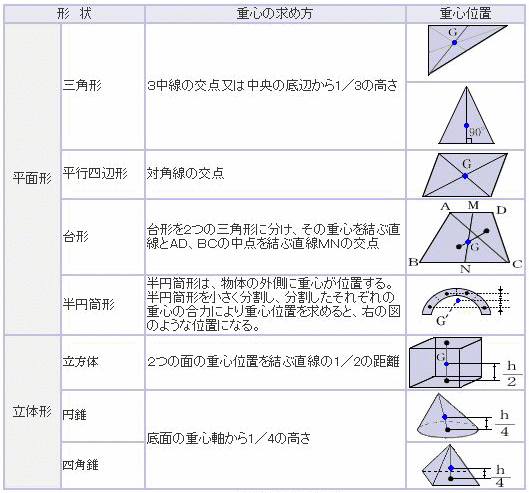
平面形や立体形等の基本形の重心位置の求め方は、表に示す通りである。