


物理学における運動とは、物体の位置関係が変化することと定義されています。アイザック ニュートンはプリンキピア(自然哲学の数学的諸原理)に運動の法則について記述しています。現代の物理学では、我々が日常的に扱うスケールでニュートン力学は有効理論であると考えられています。
ある物体が他の物体に対してその位置を変えることを「物体の運動」という。道路を走行している乗物に乗っている人は、その乗物に対しては静止しているが、道路に対しては運動している。したがって、運動は、何に対して運動しているのかという基準を定める必要がある。我々の日常生活においては、この地球の大地を基準として運動を捉えている。

等速運動とは、たとえば電車がレールの上を1秒間に10m、10秒間に100mの速度で走行する物体の運動である。等速運動は、どの時間においても同じ速度を示し、平均速度と瞬間速度の値が等しい。また、等速運動を行っている物体は、負(−)の加速度を与えると停止させることができる。不等速運動とは、速度ゼロの状態から走り始め、交通の流れに合わせて走行し、速度を落して停車する自動車のような運動をいう。
物体が単位時間に移動する距離を表したものを「速さ」といい、一定時間に進む距離の大小によって速い又は遅いという。速さと速度は、一般に同義語として扱われているが、厳密には速さと速度は区別される。毎時50kmで走っているというように、移動量だけを示す場合は速さという。速度は、北に向かって毎時50kmで走っているというように、方向と速さを示す。物体の速さは、次の式で求めることができる。ただし、不等速運動の場合は、速度が一定でないため、平均の速さを表す。速さには、次のような単位が用いられている。
● センチメートル毎秒cm/s
● メートル毎秒m/s
m/sのsは、英語のsecondの一文字を付けたものである。なお、m/secとする場合もある。
● メートル毎分m/min
● キロメートル毎時km/h
<例題 1>
作業半径12mのジブが2分間に1回転する時、ジブ先端の1分間の周速度(メートル毎分)の求め方。ジブ先端の円周は、半径×2×3.14で求めることができる。したがって、作業半径12mのジブ先端の円周は
12×2×3.14=75.36m
ジブは、2分間に1回転している。よって、1分間の周速度は

<例題 2>
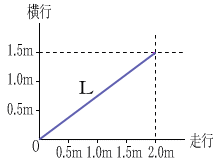
天井クレーンを2.0m/sで走行させながら、1.5m/sで横行させた時のつり荷の速度の求め方。
走行を横軸、横行を縦軸のグラフで表すと、つり荷の移動距離L は図1のように示すことが
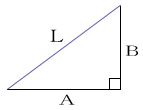
できる。また、走行距離をA、横行距離をBとした場合、A、B、Lは図2のような直角三角形を形成している。このような直角三角形には、次の式が成り立つ。
L2=A2+B2
つり荷の速度は、上記の式を用いて求めることができる。天井クレーンの走行速度と横行速度を次の式のように2乗し、この和によってつり荷の速度を2乗した値を求め、更に平方根を用いて、つり荷の速度を求める。
走行速度2+横行速度2=つり荷の速度2
ルートの計算は、電卓に6.25と入力し、ルートのボタンを押せば、つり荷の速度を簡単に求めることができるが、電卓の持ち合わせがなくても、試験問題の選択肢の数値を用いれば、つり荷の速度を容易に求められる。まず初めに、天井クレーンの走行速度と横行速度をそれぞれ2乗し、その和を求める。
2.02+1.52=2.0×2.0+1.5×1.5 =6.25
続いて、各選択肢を2 乗する。仮に選択肢の2.5m/sを2乗すると
2.52=2.5×2.5=6.25
天井クレーンの走行速度と横行速度をそれぞれ2乗した値の和と、選択肢の数値を2乗した値が一致すれば、この一致した選択肢の2.5m/sがつり荷の速度である。
物体が速度を変えながら運動する時の変化の程度を示す量を加速度という。加速度には、正(+)と負(−)の加速度があり、次第に速度を増加させる場合を正の加速度、減速させる場合を負の加速度という。t秒後に速度V1がV2になった時の加速度は、次の式で求めることができる。加速度の単位には、m/s2(メートル毎秒毎秒)やcm/s2(センチメートル毎秒毎秒)が用いられている。
<例題>
クレーンの走行速度が5 秒後に0.1m/sから0.6m/sになった時の加速度の求め方。